原始题目：剑指 Offer 35. 复杂链表的复制 (opens new window)

方法一：哈希表

遍历链表，根据就节点 $oldNode$，创建新节点 $newNode$，然后使用哈希表保存新旧节点的映射关系 $<oldNode , newNode >$。在遍历一次原始链表，当遍历到每个节点时，执行以下操作

• 根据 $oldNode$ 从哈希表中拿到对应的 $newNode$ ，拼接到新链表中。
• 根据 $oldNode.random$ 从哈希表中拿到 $newNode$ 对应的 $random$ 指针应该指向的节点。

public Node copyRandomList(Node head) {
    if (head == null) {
        return null;
    }
    // 用哈希表先建立每个旧节点与新节点的映射
    HashMap<Node, Node> map = new HashMap<>();
    Node cur = head;
    while (cur != null) {
        map.put(cur, new Node(cur.val));
        cur = cur.next;
    }
    cur = head;
    while (cur != null) {
        Node newCur = map.get(cur);
        // 找新节点的 next 和 random，它们都应该在 map 中
        // 且各自与 cur.next 和 cur.random 对应
        newCur.next = map.get(cur.next);
        newCur.random = map.get(cur.random);
        cur = cur.next;
    }
    return map.get(head);
}

复杂度分析

• 时间复杂度$O(N)$：$N$ 为链表的节点个数。哈希表的插入与搜索都是 $O(1)$ 时间的，链表的拼接也是 $O(1)$ 的。
• 空间复杂度$O(N)$：$N$ 为链表的节点个数。哈希表需要存储全部的节点。

方法二：拼接+拆分

拼接

先把新旧链表连接在同一个链表上，或者可以理解为在旧的节点后面跟着一个新的节点，新结点值等于旧的结点值，如下图中的第 $2$ 步。然后遍历拼接后的链表，找到新节点的 $random$ 指针，如下图中的第 $3$ 步

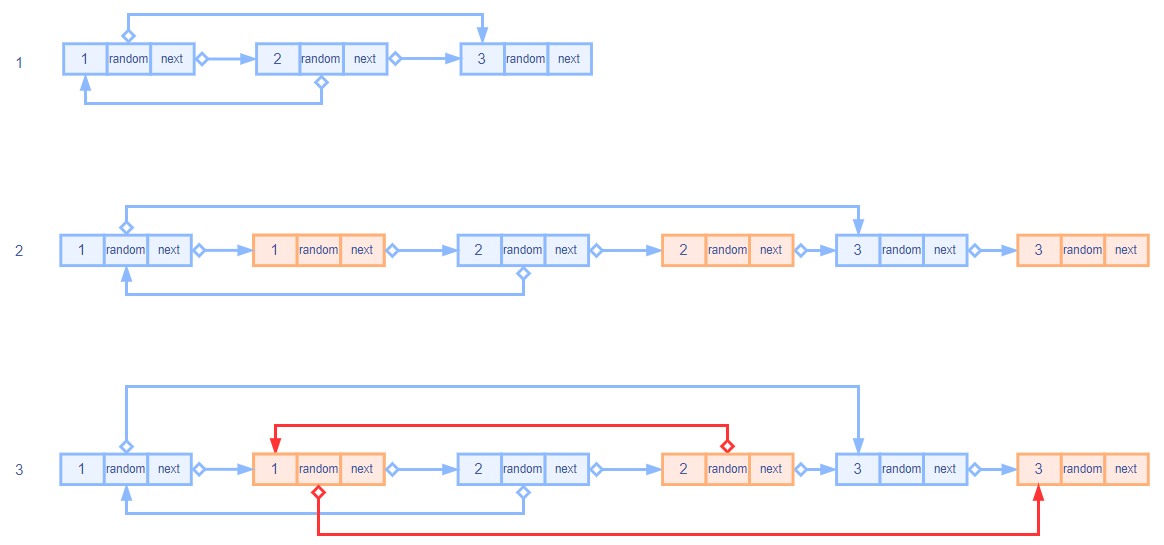
拆分

然后遍历拼接后的链表，进行拆分操作。使用双指针，$cur$ 指针指向 $head.next$，$pre$ 作为 $cur$的前驱节点指向 $head$。接下来就是 $cur$ 和 $pre$ 的 $next$ 指针都是两步走，$cur.next = cur.next.next$ 。直到 $cur$ 指针走到尾部，就结束了。

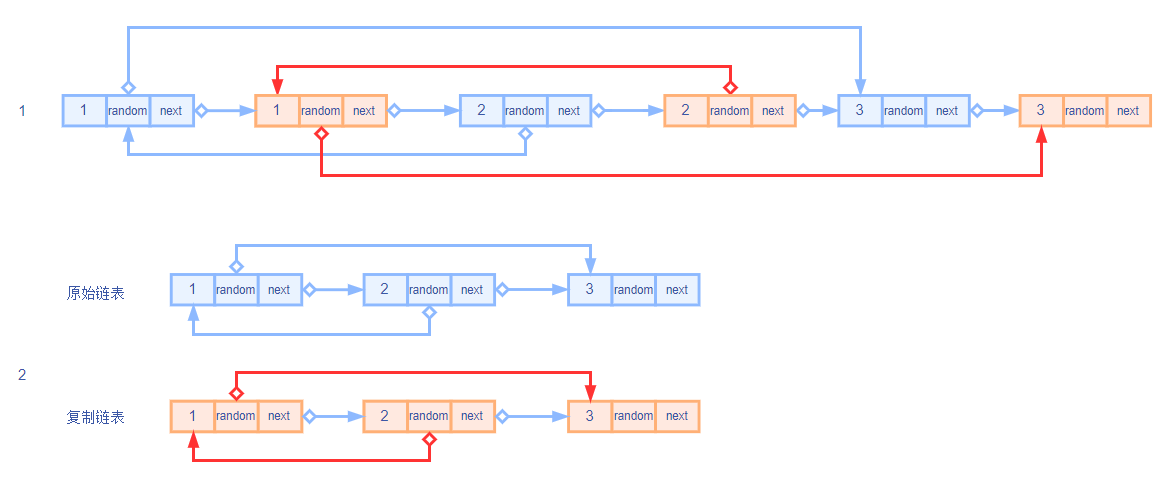
代码：

public Node copyRandomList(Node head) {
    if (head == null) {
        return null;
    }
    Node cur = head;
    // 先把新旧链表连接在同一个链表上
    // 或者可以理解为在旧的节点后面跟着一个新的节点，新结点值等于旧的结点值
    // 比如：
    // 1->2->3
    // 1->1->2->2->3->3
    while (cur != null) {
        Node newNode = new Node(cur.val);
        newNode.next = cur.next;
        cur.next = newNode;
        cur = newNode.next;
    }
    cur = head;
    // 找到新节点的 random 节点
    while (cur != null) {
        if (cur.random != null) {
            cur.next.random = cur.random.next;
        }
        cur = cur.next.next;
    }
    // 拆分链表
    cur = head.next;
    Node ans = head.next;
    Node pre = head;
    while (cur.next != null) {
        pre.next = pre.next.next;
        cur.next = cur.next.next;
        pre = pre.next;
        cur = cur.next;
    }
    // 处理原链表的尾结点
    pre.next = null;
    return ans;
}

复杂度分析

• 时间复杂度$O(N)$：$N$ 为链表的节点数目，算法中需要进行三次链表遍历，每一次占用 $O(N)$ 时间，循环中的操作占用 $O(1)$ 时间。
• 空间复杂度$O(1)$：算法中使用的变量据占用 $O(1)$ 空间。